In probability and statistics, the expectation or expected value, is the weighted average value of a random variable.
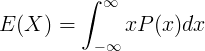
E(X) is the expectation value of the continuous random variable X
x is the value of the continuous random variable X
P(x) is the probability density function
![]()
E(X) is the expectation value of the continuous random variable X
x is the value of the continuous random variable X
P(x) is the probability mass function of X
When a is constant and X,Y are random variables:
E(aX) = aE(X)
E(X+Y) = E(X) + E(Y)
When c is constant:
E(c) = c
When X and Y are independent random variables:
E(X ⋅Y) = E(X) ⋅ E(Y)